A quadratic algorithm in its natural habitat

October 06, 2024

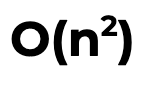
Many times during interviews (or when talking about interviews), it has been mentioned that algorithmic complexity and Big O notation is only for university studies, plus you will almost never meet algorithms during your career, where it would be useful. Is that true?

As we will see it shortly, it is not that hard to write some code, that can be very slow and painful to use under some (not so) special circumstances - at the same time, my goal is not to pick on anybody that wrote the code, just showing an example that came up for me.

This example comes from an open-source package (slackclient, version 1.3.2 to be precise), that the bot framework (errbot) we chose while implementing an internal chatbot at a previous workplace. Symptom: starting the bot takes around 1 minute and utilizes 100% of one CPU core (errbot is implemented in Python).

Investigation

Initially - no investigation, developers simply lived with slow startups. Although during everyday tasks, restarts were needed several times a day, but we had much worse problems, and it did not seem the biggest problem at that point in time. On top of that, it is possible to reload plugins in the bot framework and avoid full restarts(to be precise, it would be possible to reload plugins, though there was a different bug around it, which we also fixed eventually).

Anyways, after some time, I decided to investigate the startup time and attached a profiler to the python process. The profiler was run with something similar to: python -m cProfile errbot.

Here is the relevant part of the output¹:

         204729560 function calls (204702609 primitive calls) in 102.379 seconds

   Ordered by: cumulative time
   List reduced from 5162 to 20 due to restriction <20>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
    665/1    0.015    0.000  102.379  102.379 {built-in method builtins.exec}
...
    20180    0.075    0.000   96.856    0.005 server.py:308(attach_channel)
    20180   47.857    0.002   96.756    0.005 util.py:3(find)
203606110   48.892    0.000   48.892    0.000 channel.py:11(__eq__)
...
        6    0.000    0.000    2.320    0.387 client.py:213(rtm_read)
        6    0.000    0.000    2.320    0.387 server.py:274(websocket_safe_read)

Whoa … 203606110 calls for the __eq__ method? Why? Inspecting the source it turns out that the algorithm maintains a list of channels already added, and checks against that list sequentially every time a new channel is attached, thus ends up doing (n * (n+1) / 2) comparisons. By Big O notation, the dominant part is n² , so this is a quadratic algorithm.

In our case, 20180 channels were found - although 20180 does not sound a lot, but ( 20180 * 20179 / 2 = 203606110 ) simple string comparisons for the channel names did take a lot of time. I am sure the original author did not expect this many channels or had some other assumption why this many channels would not be checked in a real life scenario.

Conclusion

In this case, we imported the quadratic algorithm through one of our dependencies. We did not write it ourselves, but it is not a far-fetched assumption, that we could have easily done so. If we had built our chatbot when the company started out with Slack, we likely would not have noticed it either (unless the code review process caught it).

As a takeaway: always keep in mind how your code would work with a larger inputs, and design your algorithm accordingly.